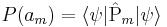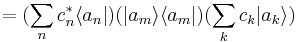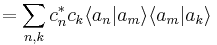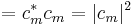Diferencia entre revisiones de «Cuaderno de cuántica - clase 2003-03-20»
De FJWiki
| Línea 9: | Línea 9: | ||
'''Nota:''' El operador proyección <math>\hat{\mathrm{P}}_n =|a_n\rangle\langle a_n|</math> Proyecta la función de onda sobre el ket <math>|a_n\rangle</math>: | '''Nota:''' El operador proyección <math>\hat{\mathrm{P}}_n =|a_n\rangle\langle a_n|</math> Proyecta la función de onda sobre el ket <math>|a_n\rangle</math>: | ||
| − | <math>\hat{\mathrm{P}}_n |a_{n'}\rangle = |a_n\rangle\langle a_n|a_{n'}\rangle</math>< | + | <math>\hat{\mathrm{P}}_n |a_{n'}\rangle = |a_n\rangle\langle a_n|a_{n'}\rangle = \delta_{n n'} |a_n\rangle</math> |
| − | <math>= \ | + | |
| + | ''Fin nota.'' | ||
| + | |||
| + | <math>\Rightarrow</math> Dado el sistema | ||
| + | |||
| + | <math>|\psi\rangle = \sum_n c_n |a_n\rangle </math> | ||
| + | |||
| + | <math>|\psi\rangle</math> siempre se puede expandir en una base completa. | ||
| + | |||
| + | Si medimos <math>\mathrm{A}</math> y obtenemos como resultado <math>a_m</math> | ||
| + | |||
| + | <math>\Rightarrow</math> <math>|\psi\rangle \longrightarrow |a_m\rangle</math> (colapsa) | ||
| + | |||
| + | con probabilidad: | ||
| + | |||
| + | <math>P(a_m)=\langle\psi|\hat{\mathrm{P}}_m|\psi\rangle</math> | ||
| + | |||
| + | <math>=(\sum_n c_n^* \langle a_n|)(|a_m\rangle\langle a_m|)(\sum_k c_k |a_k\rangle)</math> | ||
| + | |||
| + | <math>=\sum_{n,k} c_n^* c_k \langle a_n|a_m\rangle\langle a_m|a_k\rangle</math> | ||
| + | |||
| + | <math>= c_m^* c_m = |c_m|^2</math> | ||
| + | |||
[[Category:Cuaderno de Cuántica]] | [[Category:Cuaderno de Cuántica]] | ||
Revisión actual del 21:15 8 feb 2009
Supongamos que tenemos un operador 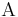 con autofunciones y autovectores
con autofunciones y autovectores 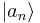 ,
, 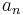
Tal que 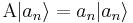
Si las funciones forman una base completa y autonormal:
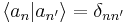
Nota: El operador proyección 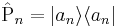 Proyecta la función de onda sobre el ket
Proyecta la función de onda sobre el ket 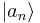 :
:
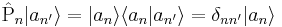
Fin nota.
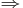 Dado el sistema
Dado el sistema
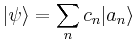
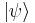 siempre se puede expandir en una base completa.
siempre se puede expandir en una base completa.
Si medimos 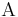 y obtenemos como resultado
y obtenemos como resultado 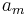
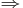
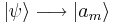 (colapsa)
(colapsa)
con probabilidad: