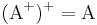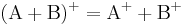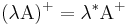Cuaderno de cuántica - clase 2003-03-18
Contenido
Postulados de la mecánica cuántica
Estado físico: 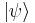 descrito por Ket.
descrito por Ket.
fase relativa: sin significado físico fase global: no sirve
Asociado a cada Ket hay un Bra
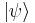
|

|
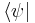
|
| Ket | Bra | |
Vive en el espacio dual 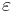
|
Vive en el espacio dual 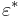
|
Los Bra son funcionales que actúan sobre los Kets:
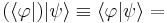 # complejo
# complejo
al sánguche: 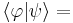 producto interno.
producto interno.
- El producto interno es lineal:
Si
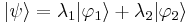 ,
, 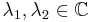
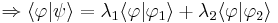
- Para pasar de Ket a Bra
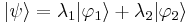 ,
, 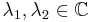
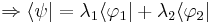
Operadores Lineales
Un operador 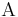 ó
ó 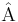
en general lleva un Ket a otro Ket:

y además

en general no conmutan
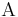 y
y 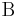 operadores
operadores
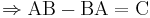
![\Rightarrow [\mathrm{A},\mathrm{B}] = \mathrm{C}](/wiki/images/math/f/1/5/f156a21c6eb1583d8a61431a952ada5a.png) conmutador
conmutador
Operadores Lineales sobre los Bra
Digamos que existe un Ket 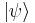 y tenemos el bra
y tenemos el bra 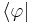

Si hacemos el producto interno:
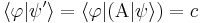
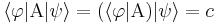
Al aplicar un operador sobre un Bra
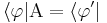
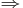 es lo mismo
es lo mismo

Paso de Kets a Bras
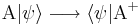
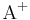 es el operador adjunto de
es el operador adjunto de 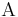 .
.
Propiedades
Demostración de 4.
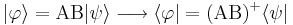

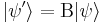 (*)
(*)
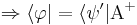
y además de (*) 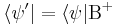
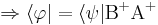
por lo tanto 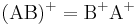
Operador hermítico
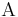 es hermítico si
es hermítico si 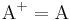
Autovalores y autovectores
Si tenemos op 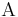 tal que
tal que
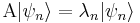
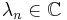
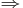 se dice que
se dice que 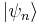 es una autofunción de
es una autofunción de 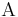 con autovalor
con autovalor 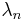
Nota
Si 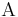 es un operador hermítico
es un operador hermítico
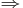 sus autovalores son reales.
sus autovalores son reales.
Demostración:
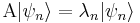
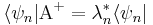
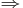
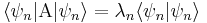
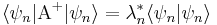
como 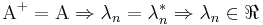
Observables
Un observable es una propiedad de un sistema que en un principio se puede medir. En mecánica cuántica se le asocia un operador hermítico.
i.e. 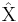 ,
, 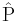 ,
, 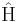
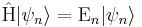
donde 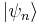 es una autofunción de
es una autofunción de 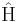
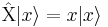
Colapso de la función de onda
Cuando un sistema es medido, la función de onda del sistema colapsa a una de las autofunciones del obervable, dando como resultado de la medición el autovalor correspondiente.